by Rafael C. Caruso, MD
On June 2019, a group of AAAP members met in Peyton Hall to attend a two-day celestial navigation course, which I found most enjoyable. The course was taught by Frank Reed, the navigation instructor who currently teaches all navigation classes offered by the Mystic Seaport in Mystic, Connecticut, a maritime museum well worth visiting.
The objective of this short article is to describe an attempt to determine local latitude and longitude by an observation of the noon sun, and its elegant theoretical background. These measurements are, in a way, a type of astrometry, the earliest form of astronomy. As this was my first such measurement, I opted to carry it out on from a stationary position on dry land rather than aboard a moving vessel (the fact that I do not own a yacht also played a role in that decision). The boardwalk in Belmar, New Jersey, provided a very convenient “deck” from which to observe the sun and the horizon on Saturday, November 16, 2019, a sunny and blustery day.
1. Requirements
This determination required three equally essential pieces of information. The devices used in this case to obtain this information are shown in Figure 1.
1. A measurement of the sun’s altitude (H) above the horizon al local noon.
The nautical sextant allows an observer to align the images of sun and horizon, and measure the angle between them. A Freiberger drum sextant, manufactured in 1984 in what was then East Germany was used. Its drum micrometer is calibrated in increments of 1 minute of arc, which allows estimating measurements to about 0.1 to 0.2 minutes of arc.
2. Precise timing of these measurements.
A wristwatch with quartz movement, set to Universal time (UT) earlier on the same day, was used in this case. UT may be obtained from the US Naval Observatory Master Clock by dialing (202) 762-1401. Since no assistant was at hand, a mechanical stopwatch was used to measure the time elapsed between each sextant measurement and its corresponding wristwatch reading.
3. A knowledge of the sun’s coordinates at the time of measurement.
The Nautical Almanac, an annual publication, lists the sun’s coordinates for every hour of every day of a given year, among much other information for celestial navigation. The Almanac is published jointly by the US Naval Observatory and the British Nautical Almanac Office. A free version containing the same information is also available online (https://thenauticalalmanac.com)

Figure 1. Sextant, timepiece(s), and Nautical Almanac. This triad provides all the information required to find latitude and longitude (photo by the author).
2. Shooting the Sun
At the moment of local noon, when the sun reaches its highest altitude, the sun crosses the observer’s meridian. This fact is reflected in the etymology of the word, which is derived from “meridies”, Latin for “noon”. For an observer is in a mid-northern latitude, the sun is then due south (conversely, for an observer is in a mid-southern latitude, the sun is due north).
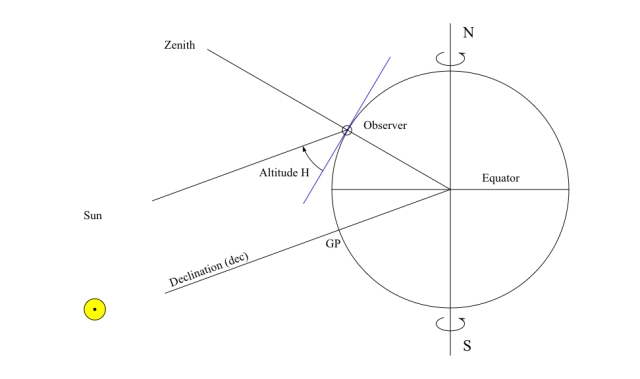
Figure 2. Diagram of a vertical section of the Earth, showing the relative locations of an observer and of the sun’s geographic position (GP) when the sun in over the observer’s meridian. Redrawn with modifications from Prinet(1).
Figure 2 shows the position of an observer, depicted as a small circle on the surface of the Earth. Latitude and longitude are unknown to this observer, but we shall assume the observer does know that he or she is north of the equator. As this measurement takes place in November, the point on the Earth’s surface where the sun is at the zenith (called the geographic position (GP) of the sun), is south of the equator. The blue line tangent to the Earth’s surface is his or her horizon, which is perpendicular to the observer’s zenith. Given the very large distance between the sun and the Earth, all the sun’s rays fall on the Earth essentially parallel to each other, both at the geographic position of the sun and at the observer’s position.
All the observer does now is to use a sextant to measure the angle of altitude H of the noon sun with respect to the horizon, and to record the exact time of this measurement. As mentioned above, and particularly since the observer may have only an approximate knowledge of the time of local noon, an ideal way to do this to take sun sights starting while the sun’s altitude is still increasing (before noon) and continuing to do so every few minutes until it begins its decline (after noon).
3. Analyzing altitude data
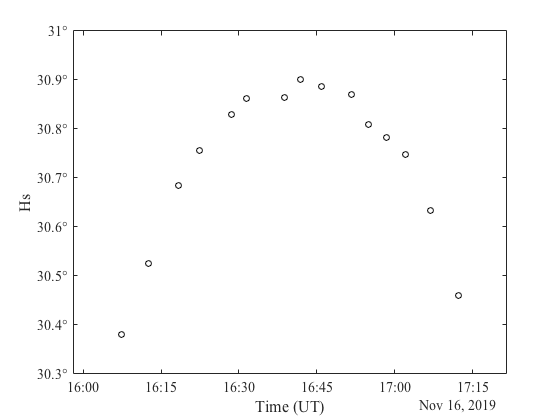
Figure 3. Graph of the sun’s altitude as measured with a sextant (Hs) as a function of coordinated universal time (UT)
A graph of the measurements just obtained is shown in figure 3, a plot of altitude (Hs, which refers to altitude H measured with sextant s) as a function of universal time UT. Universal time is equivalent to Greenwich meridian time GMT for a civil day starting at midnight in the prime meridian. In the course of about an hour, from16:15 to 17:15, the sun’s altitude described an arc of an amplitude of 0.5 degrees, with a maximum at local apparent noon. The plot shows that local noon on November 16 occurred slightly before 16:45 hours UT, and that at that moment, the sun’s altitude read from the sextant scale was approximately 30.9 degrees (30° 54’ of arc).
Celestial navigation textbooks 1-3 recommend tracing a smooth curve through the data points to determine the peak altitude at local noon by inspection. I opted to use a numerical approach, which I have not seen described in navigation manuals, though I assume has been used more than once in the past, since it is quite straightforward. As these data points describe a curve similar to a parabola, one can fit a parabolic function through them and find the function’s equation

Figure 4. Graph of the data points plotted in figure 3, after fitting a quadratic function (a parabola), and its equation. Fractions of UT hours are expressed as decimal fractions.
From the parabola, one can calculate:
a. The time of local noon, obtained from the time value corresponding to the peak or maximum of the curve. In this case, local noon was at 16.693 hours UT (16h 41m 37s).
b. The sextant reading corresponding to this time, even if the sun’s altitude was not measured exactly then. This is just the highest Hs value of the curve, which is 30.91° (30° 54.5’).
Both values are similar to those estimated by inspection of the graph. The details of this calculation are described in Appendix 1.
Before using this value to calculate a geographic position, some corrections have to be applied to it, to account for the conditions in which the sextant measurement was made. The reasons underlying this requirement are listed in Appendix 2. After these operations were carried out, the sextant altitude value Hs (30° 54.5’) was corrected to an “observed altitude” value Ho of 31° 6.5’.
4. Calculating latitude
This calculation relies of the fact that the observer and the sun are on the same meridian at the time of local noon. As mentioned above, the observer knows that he or she is north of the equator, and knows that the November sun is south of the celestial equator. Therefore, their relative positions on opposite hemispheres are as depicted in Figure 5.

Figure 5. Diagram of a vertical section of the Earth, showing the three angles required for a calculation of latitude (ZD, dec, lat). Redrawn with modifications from Prinet(1).
This figure shows that the known value the sun’s altitude H above the horizon allows us to calculate the angle between the sun’s position and the zenith. This is called the zenith distance ZD, which is simply 90° – H. In our case, ZD is 90° – 31° 6.5’ = 58° 53.5’.
The angle subtended by the larger arc drawn “inside” the diagram of the earth is also equal to ZD, since the sun’s rays are parallel for our purposes. The figure shows that this angle ZD can be visualized as the sum of two angles, the sun’s declination (dec) and the observer’s latitude (Lat).
(As an aside, it’s worth noting that the configuration of these three angles (ZD, dec, and Lat) may be different for other possible relative positions of observer and noon sun, but the latitude calculation always involves a combination of all three of them. I find that drawing a diagram of these angles is a more intuitive and less error prone approach than using any mnemonic).
Therefore, knowing the sun’s declination at local noon allows calculating the observer’s latitude. This is where the Nautical Almanac becomes essential.

Figure 6. Excerpt of a page of the Nautical Almanac for 2019, which shows the sun’s coordinates for every hour of Saturday, November 16.
The relevant section of the Nautical Almanac page for Saturday, November 16, 2019 is shown in figure 6. The almanac lists sun declination values for every hour of the day. Note that declination values are designated by convention as N(orth) or S(outh), rather than as the positive or negative values, the notation used in astronomy. The table entries outlined in red indicate that declination was S 18° 46.0’ at 16:00 hs and S 18° 46.7’ at 17:00 hs. What we need to know is the sun’s declination at 16h 41m 37s UT, which may be obtained by interpolation as S 18° 46.5’. The observer’s latitude is therefore:
Latitude = ZD – dec = 58° 53.5’ – 18° 46.5’ = 40° 7’ North
6. Estimating longitude
Although there are more accurate celestial navigation methods for the calculation longitude, a measurement of the time of local noon may also be used to estimate longitude. This estimation relies on the fact that the geographic position (GP) of the sun changes during the day (see figure 7). At local noon at longitude 0°, the sun’s GP is at some point on the Greenwich meridian. As the Earth rotates, the sun’s GP moves westward at a rate of 15° per hour, and completes a whole rotation of 360° in 24 hours. The angle between the Greenwich meridian and the meridian over which the sun’s GP has moved is called the Greenwich hour angle (GHA) of the sun. This angle is measured westward from the Greenwich meridian, from 0° to nearly 360°. In the Western hemisphere, local noon occurs later than at longitude 0°, proportionally to the distance in longitude from the Greenwich meridian. Therefore, longitude is equal to the Greenwich hour angle of the sun at local noon2.

Figure 7. Diagram of the Earth as a sphere, showing the Greenwich hour angle (GHA), increasing as the GP of the sun circles westward from the prime meridian. Redrawn with modifications from Karl (2)
To use this fact to estimate longitude, one also relies on the Nautical Almanac. The Almanac lists the GHA of the sun (and other celestial bodies) for every hour of each day. The Almanac excerpt in figure 6 shows that the sun’s GHA was 63° 49.2’ at 16:00 hours UT. Since GHA is between 0° and 180°, longitude is West of the Greenwich meridian. What we wish to know is the GHA value at the time of local noon, i.e., at 16h 41m 37s. Since we know that GHA increases at 15° per hour, or 0.25° per minute, it has increased 10° 23.4’ in the 41m 37s after 16:00 hours. Therefore, we can conclude that
Longitude = 63° 49.2’ + 10° 23.4’ = 73° 72.6’ = 74° 12.6’ West
7. Checking coordinate accuracy
At the end of this exercise, we have reached the conclusion that our coordinates are:
Latitude: North 40° 7’
Longitude: West 74° 12.6’
How accurate is this result? In these days, celestial navigation may be used as a backup if satellite navigation systems such as GPS fail, as it relies on different and independent information. But we may also use GPS as a way to check our celestial navigation results, using these more accurate values as the equivalent of “the answer on the back of the book” in a college math textbook.
The National Oceanic and Atmospheric Administration’s online solar calculator4 lists GPS coordinates of any selected location on Earth, in addition to giving solar position for any time at that location. For our location on the Belmar boardwalk, these coordinates are:
Latitude: North 40° 10.3’
Longitude: West 74° 0.9’
As one minute of latitude was historically equivalent to one nautical mile, our error of 3.3’ in latitude is approximately equivalent to a distance of 3.3 nautical miles.
The length of one minute of longitude varies with latitude, from a maximum of about one nautical mile at the equator, to a vanishingly small distance at the poles. At a latitude of 40°, a minute of arc spans approximately 0.77 nm. This implies that our error of 11.7’ in longitude is approximately equivalent to a distance of 9 nautical miles. The roughly three-fold difference between the longitude error and the latitude error is not surprising, since the method used here to determine longitude is not an ideal one, and gives only an approximate estimate of longitude.
The great circle distance between the celestial navigation coordinates and the GPS coordinates, obtained with a great circle calculator5, is 9.56 nautical miles.
In this way, knowing an angle, a time, and having access to data which relate this angle to this time, it is possible to measure latitude and estimate longitude by the noon sun. Celestial navigation is no longer the most advanced technique to find one’s position, but remains a beautiful achievement of the human mind, and provides a perception of the motions of the earth and sky that is most appealing for an amateur astronomer.
Appendix 1. Fitting a parabola
Numerical routines for fitting a parabola, or any other polynomial function, to data points are included in spreadsheet programs (e.g., Microsoft Excel, or the open source Libre Office), in graphing programs (e.g., Kaleidagraph), and in numerical analysis packages (e.g., Matlab, or the open source Octave). The best fitting parabola for our data points is shown in Figure 4, in which fractions of UT hours are expressed not as minutes but as decimal fractions, which are required by the numerical routine used. The curve-fitting program also yielded the equation of this parabola:
− 1.59 t2 + 53.02 t – 411.58
This equation may now be used to find the time of local noon, which is the time t for the maximum Hs value. For this purpose, one can follow the usual approach to find a maximum of a function. This involves calculating the first derivative of the function:
− 3.18 t + 53.02
The maximum t value is obtained by setting the first derivative to zero and solving for t.
In this way, one can determine that local noon occurred at 16.693 hours UT (16h 41m 37s). Finally, one can calculate the sextant reading corresponding to the exact time of local noon. This is just the peak Hs value of the curve, and can be obtained by substituting the peak time (16.693) in the equation of the curve. This results in a value of 30.910° (30° 54.5’) for Hs.
Appendix 2. Applying corrections
This altitude value as measured with a sextant needs to be corrected, to account for the following facts:
- A calibrated sextant may still have a minimal residual error in its angular measurement (which has to be added or subtracted from a reading).
- The observer is not at horizon level, but rather at a variable known height above it (in this case, on a modestly elevated boardwalk, 3.2 m (10.6 ft) above sea level).
- Aligning the lower limb of the sun with the horizon yields a more accurate measurement than aligning its center, which is the almanac-tabulated value.
- The atmosphere refracts rays of light from the sun. This effect is greater if the sun is close to the horizon, and minimal if it is close to the zenith.
- Sun sights are taken from the surface of the Earth rather than from its center. The resulting small parallax error is greater if the sun is close to the horizon.
Performing these corrections is considerably simpler that it may seem after reading this list. The observer is able to determine the angular measurement error (known as the index error) of his or her sextant (in this case, 0.3 min had to be added to the reading). The Nautical Almanac contains tables to perform the remaining four corrections. Alternatively, formulas for the same purpose are readily available, and may be entered on a spreadsheet program for ease of use.
References
- Dominique Prinet, Celestial navigation using sight reduction tables Pub. No 249. Friesen Press, Victoria, BC, 2018
- John Karl, Celestial Navigation in the GPS age. Paradise Cay Publications, Arcata, CA, 2011
- David Burch, Celestial Navigation, a complete home study course. Starpath Publications, Seattle, WA, 2019
- NOAA National Oceanic and Atmospheric Administration. Online solar calculator (https://www.esrl.noaa.gov/gmd/grad/solcalc/)
- Ed Williams. Great circle calculator (http://edwilliams.org/gccalc.htm)

